很多同学在复习是反馈.,自己学了数量关系公式,但是实际做题中还是耗费了很多时间怎么办?
接下来河北公务员考试网给大家整理了常见的9大题型的秒杀公式,手把手教你提升做题的效率!
1.和倍问题
【问题描述】
已知两数之和及倍数关系,可快速得出这两数。
【秒杀公式】
大+小=和;大=倍×小,
则:小=和÷(倍+1)﹔大=倍×小=和-小。

【解题思路】
甲比乙大,甲乙之和=60,甲乙的倍数=3;则得出:乙=60÷(3+1)=15千米/小时,甲=60-15=45千米/小时。

【解题思路】
男比女多,和=30,倍数=1.5;利用公式,则得出:
女=30÷(1.5+1) =12人,男=30-12=18人
2.差倍问题
【问题描述】
已知两数之差及倍数关系,可快速得出这两数
【秒杀公式】
大-小=差;大=倍×小,
则:小=差÷(倍-1);大=倍×小=差+小。

【解析思路】
甲-乙=30,甲÷乙=4;
利用公式,则得出:乙=30÷(4-1)=10岁,则甲=10+30=40岁。

【解析思路】
男比女多,和=30,倍数=1.5;利用公式,则得出:
女=30÷(1.5+1) =12人,男=30-12=18人。
3.和差问题
【问题描述】
已知两数之和及两数之差,可快速得出这两数。
【秒杀公式】
大+小=和;大-小=差;
则:大=(和+差)÷2;小=(和-差)÷2。

【解析思路】
已知父亲+儿子=60,父亲-儿子=30;利用公式,则得出父亲= (60+30)÷2=45岁;儿子=45-30=15岁。
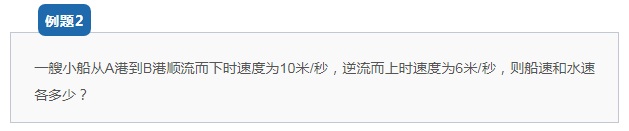
【解析思路】
已知船速+水速=10,船速-水速=6;利用公式,则得出船速=(10+6)÷2=8米/秒,水速=10-8=2米/秒。
4.日期问题
【问题描述】
若2017年7月10日星期三,则2018年7月10日星期几?
【秒杀公式】
平年:365=52×7+1,平过1;
闰年:366=52×7+2,闰过2。
(平年与闰年区分:世纪年为一百年。如果不是世纪年,年份能被4整除为闰年,有余数为平年;如果是世纪年,必须被400整除是闰年,否则是平年。)

【解析思路】
解答此类题需要知道,这一整年过的是平年的2月,还是闰年的2月。2017年3月5日至2018年3月5日过的是2018年的2月,是平年。根据公式:平过1,所以应该过1天。
则答案为:2018年3月5星期六。

【解析思路】
同样要知道2015年5月1日至2016年5月1日,过的是2016年的2月,是闰年。根据公式闰过2。
则答案为:2016年5月1日星期五。
5.植树问题
【问题描述】
在一个路段上植树,植树方式不同,棵数和段数的关系不同。
【秒杀公式】
①不封闭路段:
两端植:棵数=段数+1;
一端植:棵数=段数;
②两端都不植:棵数=段数-1;
封闭路线:棵数=段数。
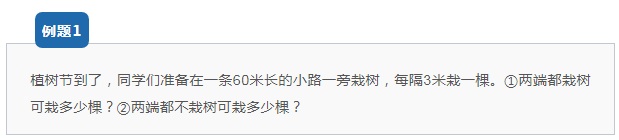
【解析思路】
①两端都种问题:段数=60÷3=20,根据公式,棵数=段数+1=20+1=21棵。
②两端都不种问题:根据公式。棵数=段数-1=20-1=19棵。

【解析思路】
─根木头锯段,相当于两端都不种。截成7段需要锯6次,则用时=6X8=48分钟。
6.方阵问题
【问题描述】
已知每一边上的数量,求方阵一圈的个数;已知每一圈的数量,求方阵一边上的个数。
【秒杀公式】
若一圈个数m,一边个数为n。则m=4n-4; n=(m+4)÷4。
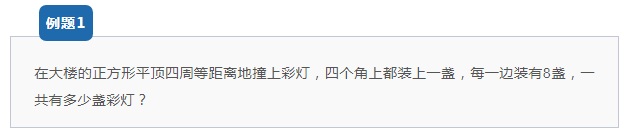
【解析思路】
此题是已知一边求一圈,一边是8盏灯,n=8。根据公式,一圈彩灯数量为:m=4n-4=4X8-4=28盏。
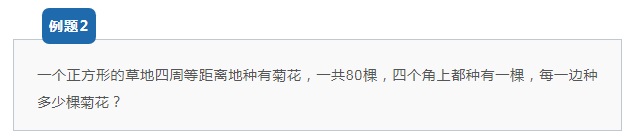
【解析思路】
已知一圈求一边,一圈共80棵,m=80,根据公式,每一边数量为: n=(m+4)÷4=(80+4)÷4=21棵。
7.火车过桥问题
【问题描述】
在火车车长和桥长已知时,根据车速求时间。在火车车长和桥长已知时,根据时间求车速。
【秒杀公式】
完全过桥:车速=(桥长+车长)÷过桥时间;
完全在桥:车速=(桥长-车长)÷过桥时间;
过大小桥:车速=(大桥-小桥)÷时间差。

【解析思路】
过山洞时间:(洞长+车长)÷车速=(500+300)÷20=40秒,
在山洞时间:(洞长-车长)÷车速=(500-300)÷20=10秒。
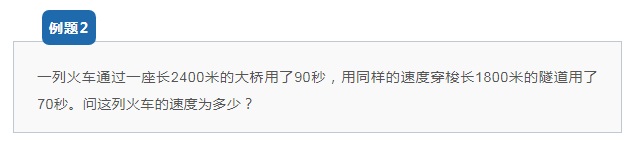
【解析思路】
过大小桥问题:车速=(大桥-小桥)÷时间差=(2400-1800)÷(90-70)=30米/秒。
8.空瓶换水问题
【问题描述】
已知4个空瓶可以换一瓶饮料,则若买36瓶饮料,最多喝多少瓶?
【秒杀公式】
N空瓶换1瓶水,相当于买(N-1)喝N瓶。
解释:4空瓶换1瓶水,相当于买3喝4。所以买了36瓶,相当于买了12个3瓶,是12个4瓶。所以,最多喝36÷3x4=48瓶。
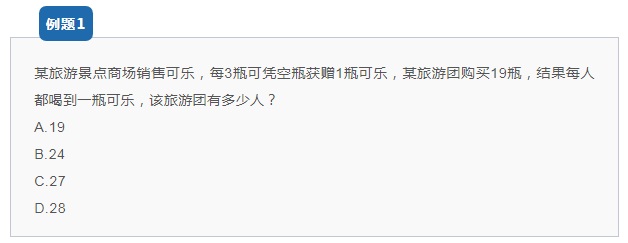
【解析思路】
问旅游团多少人,其实就是问喝了多少瓶可乐。题干可知:买3瓶可以凭空瓶获赠一瓶,即:3个空瓶换一瓶可乐。因此得出买2喝3瓶,19/2=9余1。买了9个两瓶,可以喝9个3瓶,故可以喝27瓶,再加上余下的1瓶,共可以喝28瓶。
故答案为:旅游团共有28人。
9.容斥极值问题
【问题描述】
已知N个集合A、B、C...以及全集l,求N个集合公共部分最少为多少?
【秒杀公式】
个集合之和―(N-1)倍合集;
两集合交集最少:A+B-l;
三集合交集最少:A+B+C-2l;
四集合交集最少:A+B+C+D-3l。
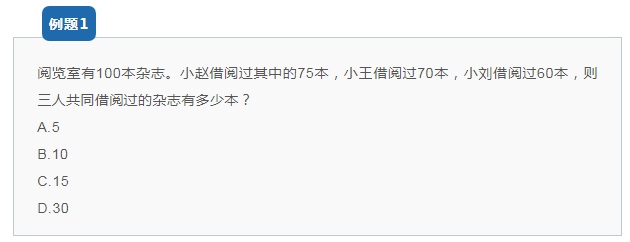
【解析思路】
从题干可知。是三集合交集最少,利用公式,三人共同借过的杂志数最少有:A+B+C-2l=75+70+60-2×100=5本。故答案选A。
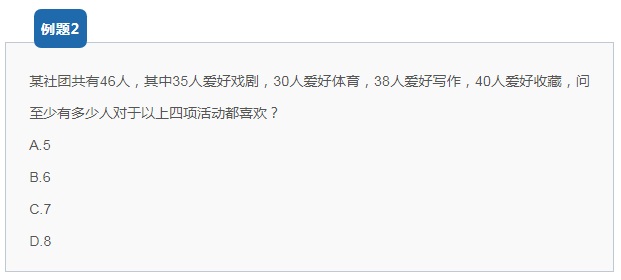
【解析思路】
从题干可知,是四集合交集最少,利用公式,四项运动都喜欢的人至少有:
A+B+C+D-3l=35+30+38+40-3X46=5人。
故答案选A。
通过以上数量关系的9大秒杀公式及例题讲解,是不是觉得很好掌握呢?这就是“知识与思维的妙用”。善于运用干中隐含的特征及已知条件来提升自己对题型的灵敏度,从而快速解题。
当然,要具备这样的能力,还是一句老话送给大家:扎实的基本功是硬道理!平时在学习数学运算时,要侧重于基础知识的掌握,在练习时多思考、多总结,遇到类似题目的时候才能够真正举一反三!

2022年河北省考时间推迟,笔试不能懈怠,现在就要抓紧备考~












