1.请从理论或逻辑的角度在后面的空格中填人后续字母或数字：
①A，D，G，J，（ ）
②21，20，18，15，11，（ ）
③8，6，7，5，6，4，（ ）
④18，l0，6，4，（ ）
2.如下表，从左到右在每个小格子中都填人一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第2011个格子中的数为（ ）。
A.3 B.2 C.0 D.一1
3.填在下面各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（ ）
A.38 B.52 C.66 D.74
4.观察下面几组数：
①1，3，5，7，9，11113，15，…
②2，5，8，11，14，17，20，23，…
③7，13，19，25，31，37，43，49，…
这三组数具有共同的特点。
现在有上述特点的一组数，并知道第一个数是3，第三个数是11，则其第n个数为（ ） 。
A.8n－5 B.n2+2 C.4n－1 D.2n2－4n+5
5.23，33，43分别可以按如图所示方式“分裂”成2个、3个和4个连续奇数的和，63也能按此规律进行“分裂”，则63“分裂”出的奇数中最大的是（ ）。
A.41 B.39 C.31 D.29
河北公务员网（http://www.hebeigwy.org/）解析 题目或解析有误，我要纠错。
1.M；6；5；3【解析】①按26个英文字母的顺序，间隔2个英文字母；②由题中数据可得，前一项与后一项之差是公差为l的等差数列；③奇数位后面一个数比前面一个数少1，偶数位后面一个数比前面一个数少1；④由题中数据可得，前一项与后一项之差是公比为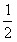
的等比数列。
2.A【解析】此题考查的是数字的变化类问题，解题的关键是先由已知求出、、c，再找出规律求出答案。已知其中任意三个相邻格子中所填整数之和都相等，则3++=，所以按要求排列顺序为3，一1，3，一1，…再结合已知表得：2，所以每个小格子中都填入一个整数后排列是：3，一1，2，3，一1，2，…得到：每3个数一个循环，则2011÷3=670…1，因此第2011个格子中的数为3。故选A。
3.D【解析】分析前三个正方形可知，规律为右上和左下两个数的积减左上的数等于右下的数，且左上、左下、右上三个数成公差为2的等差数列。因此，图中阴影部分的两个数分别是：左下是8，右上是10。8×10－6=74，故选D。
4.C【解析】分析数据可得：第一个数是3，第三个数是11，则第二个数为7，即每个数比前一个大4，故其第n个数为4n一1。故选C。
5.A【解析】本题的关键是从前面的三个分解里找到相应的规律（n2+n－1），并依据规律解题。23有2个奇数相加，最大的为22+1，33有3个奇数相加，最大的为32+2，43有4个奇数相加，最大的为42+3，那么63就有6个奇数相加，最大的为62+5=41。故选A。
