1.观察表一，寻找规律，表二、表三、表四分别是从表一中截取的一部分，其中、、c的值分别为（     ）。

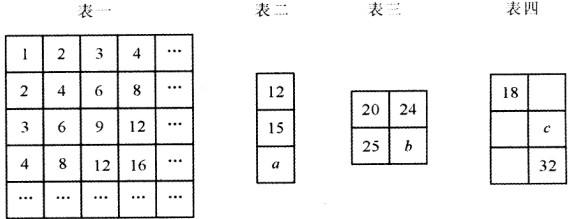
　　A.20、29、30      B.18、30、26      C.l8、20、26      D.l8、30、28

　　2.世界上着名的莱布尼茨三角形如图所示，则排在第10行从左边数第3个位置上的数是（   ）

　　
　　3.观察下列三角形数阵：则第50行的最后一个数是（     ）。

　　
　　A.1225          B.1260     C.1270       D.1275

　　4.计算：2¹-1=1，2²-1=3，2^3-1=7，2⁴-1=15，2⁵-1=31，···，归纳各计算结果中的个位数字规律，猜测2²⁰⁰⁶－1的个位数字是（      ）。

　　A.1         B.3       C.7        D.5

　　5.请你认真观察和分析图中数字的变化规律，由此得到图中所缺的数字是（     ）。

　　A.32    B.29     C.25         D.23

　　河北公务员考试网（http://www.hebeigwy.org/）解析　题目或解析有误，我要纠错。

　　1.D【解析】此题只要找出截取表一的那部分，并找出其规律即可解。表二截取的是其中的一列：上下两个数字的差相等，所以=15+3=18。表三截取的是两行两列的相邻的四个数字：右边一列数字的差应比左边一列数字的差大1，所以b=24+25－20+1=30。表四中截取的是三行两列中的6个数字：18是3的6倍，则c应是4的7倍，即28。故选D。

　　2.B【解析】注意根据所给的特殊数据发现规律。观察发现：分子总是l，第n行的第一个数的分母就是n，第二个数的分母是第一个数的（n－1）倍，第三个数的分母是第二个数的分母的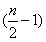倍。则第10行从左边数第3个位置上的数是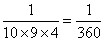，故选B。

　　3.D【解析】第一行的最后一个数是1，第二行的最后一个数是l十2=3，第三行的最后一个数是1十2十3=6……，依此类推，第n行的最后一个数是1+2+3+…+n=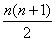。当n=50时，原式=1275。故选D。

　　4.B【解析】可根据题意得出个位数字周期为4，再用2006除以周期看余数为多少即可知道本题的答案。依题意得T=4，2006÷4=501…2，因此2²⁰⁰⁶-1的个位数字与22-1的个位数字相同。故选B。

　　5.B【解析】解答本题，应从较小的数入手，得到两个数相差的规律。1和5之间相差2²，5和13之间相差2³，那么后一个数应是13+2⁴=29。故选B。