1、有一排长椅总共有65个座位，其中已经有些座位上有人就坐。现在又有一人准备找一个位置就坐，但是此人发现，无论怎么选择座位，都会与已经就坐的人相邻。问原来至少已经有多少人就坐？（    ）

　　A.13              B.17              C.22              D.33

　　2、

　　3、254个志愿者来自不同的单位，任意两个单位的志愿者人数之和不少于20人，且任意两个单位志愿者的人数不同，问这些志愿者所属的单位数最多有几个？（    ）

　　A.17              B.15              C.14              D.12

　　4、A、B、C、D、E是5个不同的整数，两两相加的和共有8个不同的数值，分别是17、25、28、31、34、39、42、45，则这5个数中能被6整除的有几个？（    ）

　　A.0              B.1              C.2              D.3

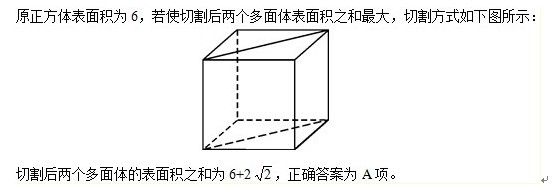
　　5、

　　河北公务员网（http://www.hebeigwy.org/）解析　题目或解析有误，我要纠错。

　　1.【解析】C。由题意，此人无论怎么坐都会与已就坐的人相邻，因此，长椅除了首尾两个位置，中间的空位不能超过2个，首尾的空位不能超过1个，设第一个空位上有人，每三个座位上有1人，63个座位共有21人，再加上最后的位置上必须再坐1人，才能保证此人无论怎么坐都会与已就坐的人相邻，所以，原来至少已经有21+1=22（人）就坐。正确答案为C项。

　　2. 【解析】A。

　　3. 【解析】B。

　　4. 【解析】C。设A＜B＜C＜D＜E，则必有A+B=17，A+C=25，C+E=42，D+E=45。还剩下4个数28、31、34、39。由于（A+B）+（A+C）+（B+C）＝2（A＋B+C）是偶数，A+B＝17，A+C＝25，所以B+C也一定是偶数，于是有B+C＝28或34，又因为比B+C大的不同的和值至少有4个（B+D,D+C,C+E,D+E），故可排除34，所以B+C＝28，结合前面所列方程，可求出A=7，B=10,C=18,D=21,E=24。故选C。

　　5. 【解析】C。