1.四个足球队进行单循环比赛，每两队都要赛一场。如果踢平，每队各得1分，否则胜队得3分，负队得0分。比赛结果，各队的总得分恰好是四个连续的自然数。问：输给第-名的队的总分是多少？ （ ）
A.1分 B.2分 C.3分 D.4分
2.一个四位数，千位为3,十位为2,且能被55整除，则这个四位数最大是多少？ （ ）
A.3520 B.3025 C.3925 D.3820
3.在1至100的自然数中，不能被2整除且不能被3整除且不能被5整除的数共有多少个？ （ ）
A.23个 B.26个 C.27个 D.74个
4.某年级若干个班出去植树，已知各班人数相等，且女生人数均为男生人数的7/18,而年级主任叫走了1班一半的学生，且都是男生，此时女生人数是剩余男生人数的8/17,则参加植树的共有多少个班？（）
A.3个 B.4个 C.5个 D.6个
5.某种细菌分裂生殖方式如下：一个成熟的细菌经过6小时能分裂成1个新细菌和一个成熟的细菌，这新细菌经过12小时能成长为一个成熟的细菌。在一次实验中，研究员在某天中午12时将一个刚分裂出来的新细菌单独放入培养皿中，若干后天的下午3时观察到细菌数目变为60个，这期间经过了多少夭？ （ ）
A.1天 B.2天 C.3天 D.4天
河北公务员考试网（http://www.hebeigwy.org/）解析 题目或解析有误，我要纠错。
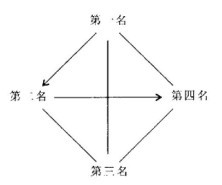
1.D【解析】首先要求出各队得多少分：四个队进行单循环赛共赛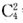
=6场，根据题意，若每场都踢平，则共2×6=l2分，若每场都分胜负，共3×6=18分，即四个球队的总分在12分到18分之间，而1+2+3=4=10,2+3+4+5=14,3+4+5+6=18,其中18分不可能（18分时，每场都分胜负，则各队得分同时被3整除），故四个球队得分分别为2,3,4,5分。故唯一的可能是第一名胜1场平2场，第二名胜1场平1场负1场，第三名平3场，第四名平2场负1场，如图所示。即只有第二名输给第一名，其总分为4分。故选D。
2.A【解析】55= 11×5,则这个四位数能同时被11和5整除，故其个位数为5或0。个位数为5时，要让它能被11整除，百位数只能为0；个位数为0时，要让它能被11整除，百位数只能为5,故这个四位数最大为3520。故选A。
3.B【解析】1至lOO的自然数中，能被2整除的数有[
]=50个，能被3整除的数[
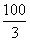]=33个，能被5整除的数有[
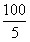]=20个，能被2整除且能被3整除的数有[
]=16个，能被5整除且能被3整除的数有[
]=6个，能被2整除且能被5整除的数有[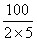
]=10个，能被2整除且能被3整除且能被5整除的数有3个，故由容斥原理，不能被2整除且不能被3整除且不能被5整除的数共有100-[50+33+20-（16+6+10）+3]=26个。故选B。
4.B【解析】根据题意，设共有n个班，各班男生人数为36,则女生人数为14,则年级主任共叫走25人，根据剩下的人数可得方程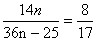
，解得=4。故选B。
5.C【解析】根据题意，从实验开始后的12小时（即新细菌变为成熟细菌时）起，细菌个数每六小时变化一次，细菌数变化情况如下表所示：
所形成的数列满足公式an=an-1+an-3（n≥4且n∈Z），故a11=60,即实验开始后经过（11-l）÷4+0.5=3天后，细菌数变为60个。故选C。
