注:本文由《河北公务员考试一本通》教材编辑部(葛珊珊)供稿。以下讲解的各种特性和巧妙的解法在《2016年河北公务员考试一本通》中都有非常系统的讲解,并在整个题型精讲和强化练习部分都可以看到一本通对此类难题讲解的巧妙之处,有需要的考生可预定一本通(预定地址:http://www.edu-book.com/tag/20)进行系统复习。一本通在编写中对行测各模块都尽可能做了细致的分析,使其解法更加实用,切实帮助考生提高在考场上的得分能力。
数学运算是公考中的必考题型,当然也绝对是难点题型。考生要么抱怨一道题完全没有思路,要么就是有了思路却栽在了复杂的计算上,在考场时间紧张的情况下,就不得不选择放弃了,是得分率较低的一个模块。其实对于公考中的数学运算模块,出题人肯定不会出特别刁钻古怪的难题,大多都是会有一定的技巧方法去快速解答的。其中数字特性法就是一剂秒杀数学运算的良药。
下面我们结合一道例题来详细介绍下如何运用数字特性法解答数学难题。
【例】
某电影院第一次卖票不到30张,每张票价41元。第二次卖票不少于30张,其中29张的票价是40元,其余的每张票30元。则这两次票房收入,共2351元。那么这两次共卖出电影票多少张( )
A.60 B.61 C.62 D.63
【错误解析】
设第一次卖了x张,第二次卖了(y+29)张,由题意可得,41x+29×40+30y=2351,即41x+30y=1191。两个未知数,一个方程,只好将各选项数据代入验证,验证过程很复杂,令很多考生望而生畏,只好随便蒙一个答案了事。
【错解门诊】
上述解析中列方程的做法是正确的。只是认识到代入验证较复杂,就应该机警地转变思路,分析所列方程有没有其他结论。对于这个式子41x+30y=1191,数学高手能看出的东西有很多,比如从尾数特性上看,30y的个位数肯定是0,因此41x的个位数肯定是1。从倍数特性上,1191这个复杂的数字,其实是能够被3整除的;结合30y也是可以被3整除,因此41x也肯定是可以被3整除的。就这样一步步缩小范围。
【正确解析】
选B。设第一次卖了x张,第二次卖了(y+29)张,由题意可得,41x+29×40+30y=2351,即41x+30y=1191。由于30y的个位数是0,则41x的个位是1,那么x的个位是1;30y、1191都是3的倍数,则41x是3的倍数,即x是3的倍数,已知x<30,则x=21,推出y=11,两次共卖出电影票x+(y+29)=61(张),B项当选。
【指点迷津】
上述例题看似复杂难解,其实运用数字特性法就可以轻而易举的进行数学秒杀。所以考生应该熟练掌握此类方法。掌握数字特性法的关键,是掌握一些最基本的数字特性规律。这就需要我们判断出什么样的题可以用数字特性法进行求解,一般当题中给出几个量之间的和(差),并且要求求出其差(和)时,简称为知和求差、知差求和;当题中给出比例关系、分数、百分数、倍数时可以考虑使用数字特性进行求解。

常见的数字特性法有奇偶特性、整除特性、尾数特性等。
一、奇偶运算基本法则
【基础】
奇数±奇数=偶数;偶数±偶数=偶数;奇数±偶数=奇数。
【推论】
1.任意两个数的和如果是奇数,那么差也是奇数;如果和是偶数,那么差也是偶数。
2.任意两个数的和或差是奇数,则两数奇偶相反;和或差是偶数,则两数奇偶相同。
二、整除判定基本法则
1.能被2、4、8、5、25、125整除的数的数字特性
能被2(或5)整除的数,末一位数字能被2(或5)整除;
能被4(或25)整除的数,末两位数字能被4(或25)整除;
能被8(或125)整除的数,末三位数字能被8(或125)整除;
一个数被2(或5)除得的余数,就是其末一位数字被2(或5)除得的余数;
一个数被4(或25)除得的余数,就是其末两位数字被4(或25)除得的余数;
一个数被8(或125)除得的余数,就是其末三位数字被8(或125)除得的余数。
2.能被3、9整除的数的数字特性
能被3(或9)整除的数,各位数字和能被3(或9)整除。
一个数被3(或9)除得的余数,就是其各位相加后被3(或9)除得的余数。
3.能被11整除的数的数字特性
能被11整除的数,奇数位的和与偶数位的和之差,能被11整除。
三、尾数特性核心判定特征
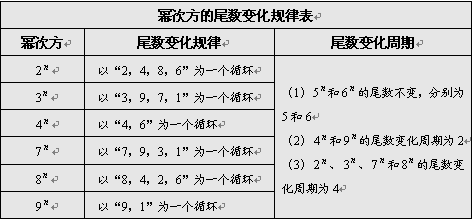
在竞争激烈的公务员考试中,平均每个试题解答不到1分钟时间,如何快速准确的解答数学运算试题,成为了备考中不可忽略的一个环节。考生应充分掌握数学特性法这一秒杀技,牢记上面所涉及的常见的数字特性。加上自己的刻苦训练,定能攻克这一模块。
>>> 点击可进入争议易错题专栏










